
СОЗДАНИЕ БЛОКА УПРАВЛЕНИЯ НА БАЗЕ НЕЧЕТКОЙ ЛОГИКИ
ЛАБОРАТОРНАЯ РАБОТА №ХЗ
по курсу "Управление в технических системах" НИИ "БАТЦА"
Москва, 2015 г.

СОЗДАНИЕ БЛОКА УПРАВЛЕНИЯ НА БАЗЕ НЕЧЕТКОЙ ЛОГИКИ
ЛАБОРАТОРНАЯ РАБОТА №ХЗ
по курсу "Управление в технических системах"
НИИ "БАТЦА"
Москва, 2015 г.
Введение:
Давненько я не брал в руки шашек.
В России большинство "русской интеллигенции" и гражданских активисток, обычно течет от иносранцев, даже если это пьяный в жопу финс ссущий на Невском проспекте, или иностранное программное обеспечение написанное индусами нанятыми за 3 копейки белым хозяином. Но я, как интеллигент в первом поколении, ватник и колорад считаю, что мы можем делать не хуже и местами даже лучше, тем более в области математического моделирования и теории автоматического управления. Еще в 2004 году, мы занимались импортозамещением и показывали, как можно средствами ПК "МВТУ" заменить Simulink для моделирования регуляторов на базе нечеткой логики. Продукт развивался и теперь он называется "SimInTech" возможности расширялись и по просьбе партии и правительства взявшего курс на "импортозамещение" мы выпускаем вторую редакцию лабораторной работы.
Некоторые несознательные товарищи, которые нам не совсем товарищи, а совсем наоборот, продажные наймиты мировой буржуазии, при выборе пакета для моделирования советуют руководствуются такими, чуждыми нашему строю, рассуждениями. "Допустим, пользователю нужно моделировать регулятор нечеткой логики. Пакет XXX имеет средства для работы с нечеткой логикой а пакет ЙЙЙ не имеет. Какой пакет выбрать?" При это подразумевается ответ, деваться некуда надо пиздить или покупать Simulink вместе с MatLab. А вот и хрен им всем с маслом. Выполнив эту лабу вы поимейте, что выбирать надо SimInTech.
Но самое интересное, мои маленькие друзья, раз партия сказала импортозамещение, то теперь американский Simulink должен идти на органы, или органы придут к тем кто его закупает, и у нас с вами появляется возможность помочь кровавому мордеру и заменить Simulink, рубанув при этом балосов. Алгоритм прост, как все гениальное, выполнив эту лабораторную работу вы поймете как можно делать библиотеки для SimInTech и теперь ваше финансовое благополучие в ваших руках. Берете с торрентов Simulink, выбираете понравившейся вам ToolBох и по образцу и подобию делаете библиотеку в SimInTech - все можно рубить капусту.
"Мы работаем как отбойный молоток,
Лабаем TollBoxы ебем MathWork"
Цель работы:
В учебниках по теории нечеткой логики часто изложение построено таким
образом, чтоб читатель охренел с первых страниц и проникся крутизной авторов,
а так же осознал собственную непроходимую тупость. Авторы уверяют, что
без знания о предикатах, коньюкции, дезьюкции, импликации и прочей
подобной поебени, изучить принципы работы управления на базе нечеткой логики
невозможною. Конечно, грязному ботану подобное изложение, может и доставляет не с
чем несравнимое райское наслаждение. Но нормальный чисто конкретный инженер или
студент скажет прямо "В жопу такое баунти" после первых
страниц. Выполнив эту лабораторную работу, Вы поймете, что
нечеткая логика, это просто как два пальца намочить, а авторы учебников просто
наводят тень на плетень, причем эта тень явно от листьев хрена и получается
полная хренотень.
Что бы понять чем отличается нечеткая логика от обычной
рассмотрим простой пример с краном. Обычная логика:
Если в кране нет воды,
значит выпили жиды.
Если в кране есть вода,
то еврей нассал туда.
Другими словами вода либо есть либо нет, а третьего
не дано и в любом случае виноваты евреи или Чубайс. Представим теперь что Вы
новый русский или старый евреи или даже сам Чубайс, а значит у Вас всегда в
кране есть и горячая и холодная вода. Залезаете Вы под душ и начинает крутить
краны. Сначала откручиваете кран с холодной водой яйца становятся квадратными от
холода, начинаете откручивать кран с горячей водой и чувствуете свою ошпаренную
жопу. Ощущаете разницу? Теперь у вас не только есть вода (или ее нет), как в
случае обычной логики, но она еще может быть, холодной, очень холодно,
нормальной, горячей или совсем кипяток. А задача управления, в данном случае привести температуру к нормальной.
Сообразительные перцы на этом месте могут меня остановить. Типа чего ты
гонишь, если известна
температура воды, то можно построить алгоритм управления открывающий нужный
кран в зависимости от текущей температуры и поддерживающий заданную температуру,
в МВТУ подобные алгоритмы делаются без всякой нечеткой логики, где здесь
особенность?
Отвечаю прямо, как есть, особенность регулирования температуры воды с помощью нечеткой
логики в жопе. Дело в том что Ваша задница не может определить температуру воды
в градусах Кельвина, Цельсия или Фаренгейта. Вы жопой чувствуете горячая вода,
холодная или нормальная и крутите краны в нужную сторону.
И вот однажды, одному кексу, которому в лом было
составлять честные алгоритмы управления, расчетные зависимости для регуляторов,
пришла в голову здравая идея. Как всегда случайно, например Ньютону яблоко в
темя шарахнуло, а этому перцу явно водой жопу обварило. Выскочил они ошпаренный
из ванны и заорал благим матом. Эврика! Что в переводе с древнегреческого
означает. Бля! Если с помощь одной только голой жопы можно с успехом регулировать
температуру воды, почему бы не попробовать такой же метод и для других задачах
управления.
Вместо того чтобы подбирать коэффициентов для всяких там ПИД регуляторов,
управление осуществляется с помощь набора правил например:
1. если вода горячая то открываем кран холодной воды;
2. если вода холодная то открываем кран горячей воды;
3. если вода холодная и кран горячей открыт полностью, то закрываем кран холодной;
4. если вода горячая и кран холодной воды открыт полностью, то закрываем кран горячей воды.
Как видим алгоритм управления
становится простым и понятным даже последнему дауну. Если все так просто, то где
здесь собака порылась? спросите вы. Отвечу, в науке и технике, при моделировании
различных процессов, как правило не используется такой чуткий и измерительный
инструмент как жопа. Есть даже поговорка железо жопой думать не научишь. Вместо интуитивно понятного сигнала "горячо" с датчиков, как
правило, приходит конкретная температура в градусах Кельвина, Цельсия или
Фаренгейта. Да и кран нужно не просто "закрывать" а указывать на какой угол
поворачивать или с какой скоростью крутить иначе тупое железо не поймет, что от
него хотят. В следующем параграфе мы и рассмотрим как эти фундаментальные непонятки разбодяжить.
Для того, чтобы можно было применять простые правила,
данные, передаваемые в блок регулирования на основе нечеткой логики, должны быть
преобразованы. Для этого предлагается следующие:
Входные и выходные преобразовываются в
лингвистические переменные. Каждая
лингвистическая переменная характеризуется набором термов. Например
лингвистическая переменная температура может иметь следующие термы
"холодно", "нормально",
"горячо". Лингвистическая
переменная уровень может иметь следующие термы: "низкий",
"нормальный", "высокий".
Лингвистическая переменная задвижка может иметь следующие термы
"открывать быстро",
"открывать медленно", "не
трогать", "закрывать
медленно", "закрывать
быстро". Каждый терм описывается своей функции принадлежности µi(x),
которая может принимать значения от 0 до 1.
Получив значение входной переменной x в
блоки нечетко логики вычисляется значения
µi(x)
каждого терма. Это процедура называется медицинским термином Фазификация.
Результатом применения правила являются величина, называемая степенью истинности, а попросту
число от 0 до 1. Что бы было понятно
рассмотрим пример: Пусть есть задвижка которая
открывается по сигналу уровня и простое правило:
Если уровень низкий то
задвижку открывать быстро.
У нас есть входная величина уровень h в
метрах. Если величина уровня стопудово низкая (µlow(h)
=
1, где
µlow(h)
- функция принадлежности для трема
низкий), или уровень стопудово не низкий ((µlow(h)
= 0), то все происходит
как и в обычной логике, степеь истинности правила принимает значение 1 или 0.
Нечеткость начинается если 0 < µlow(h)
< 1, например = 0.5. Уровень низкий, но не
очень. Соответственно и открывать задвижку нужно быстро, но не очень. В
данном правиле степень истинности равна 0.5. Подобным образом
происходит ее вычисления для каждого правила.
По научному, этот процесс называется
Активизация.
Заключения из каждого
правила собираются вместе для каждой лингвистической переменной, этот процесс
называется Аккумуляця. Например после расчета набора правил, мы получаем
результаты для лингвистической переменной задвижка:
"открывать быстро" - 0.5,
"открывать медленно" - 0.3, "не
трогать" - 0, "закрывать
медленно"-0, "закрывать
быстро"-0. Понятно,
что скорость задвижки лежит где то между медленной и быстро.
Зная степень истинности
для каждого терма выходной переменной можно рассчитать ее числовое значение. Эта
процедура называется Дефазификацией.
Таким образом работа блока управления на базе нечеткой логики может быть разбита на следующие
этапы:
2. ИСПОЛЬЗОВАНИЕ ЯЗЫКА ПРОГРАММИРОВАНИЯ В МВТУ ДЛЯ СОЗДАНИЯ РЕГУЛЯТОРА НА БАЗЕ НЕЧЕТКОЙ ЛОГИКИ.
В 2004 году в SimInTech появился новый блок -
язык программирования. Уже 10 лет как пользователю SimInTech полностью развязали руки. И если руки растут не из жопы, то любая безумная идея, случайно залетевшая в голову, может быть легко и непринужденно реализована, как говорится не отходя от кассы. Встроенный
язык программирования является настоящим языком программирования высокого
уровня, и при этом обладает всеми возможностями "Нового"
блока для задания дифференциальных уравнений в форме Коши. Кто-то может сказать, что все это дребедень, а настоящие языки
программирования это С++, Pascal, Java. Но такое может
заявить только задроченный онанист-программист который высушил остатки мозгов
работая с разным говном типа Windows GDI или SQL. Нормальным же перцем абсолютно по барабану на каком языке писать код,
главное чтоб он работал и позволял отмоделировать все что движется и шевелится
от черепахи до гравицапы.
Внешний вид SimInTech с открытым окном редактора языка программирования представлен на рис. 2.1. Новый блок
по умолчанию находится в закладке Динамические. Редактор языка
программирования открывается по двойному клику на блоке в схемном окне.
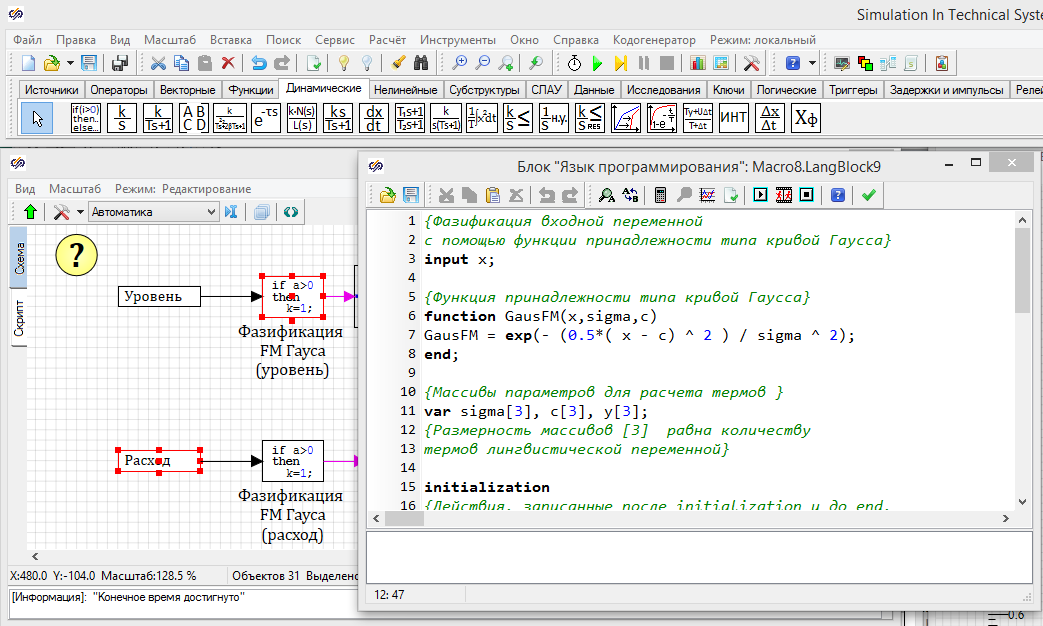
Рис. 2.1 Вид окна языка программирования
Есть два способа изучать программу читать инструкцию и работать
с программой. Второй метод получил название метод научного тыка. Чтобы оценить
как работает новый блок, давайте приступим к его юзанию, в полном соответствии с
научной методой.
Пора на чисто конкретном примере посмотреть, что можно сделать, имея встроенный язык программирования в SimInTech, да пару - тройку не совсем пропитых мозговых извилин.
Для начала займемся расчлененкой, будем расчленять исходную величину
на несколько термов, рассчитывая для каждого трема функцию принадлежности. При этом мы убедимся,
что это совсем не страшно.
Создайте новую схему автоматики и настройте параметры расчета. Установите время моделирования 20 сек. Для тех кто в танке напоминаю, что для этого нужно залезть в меню Расчет/Параметры расчета и найти строку как Конечное врем расчета. Для расчета с максимальной скоростью, на закладке "Синхронизация" снимете галочку "Синхронизировать с реальным временем" см. рис. 2.2
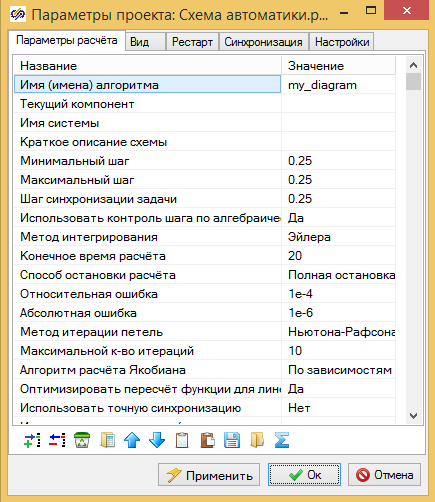
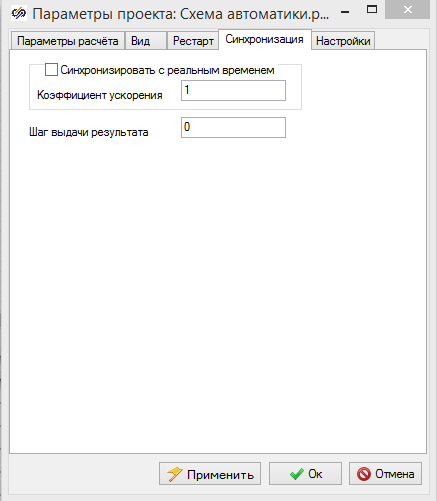
Рис. 2.2. Настройка параметров расчета.
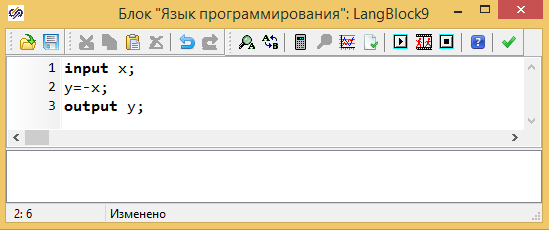
рис. 2.3. Программа блока.
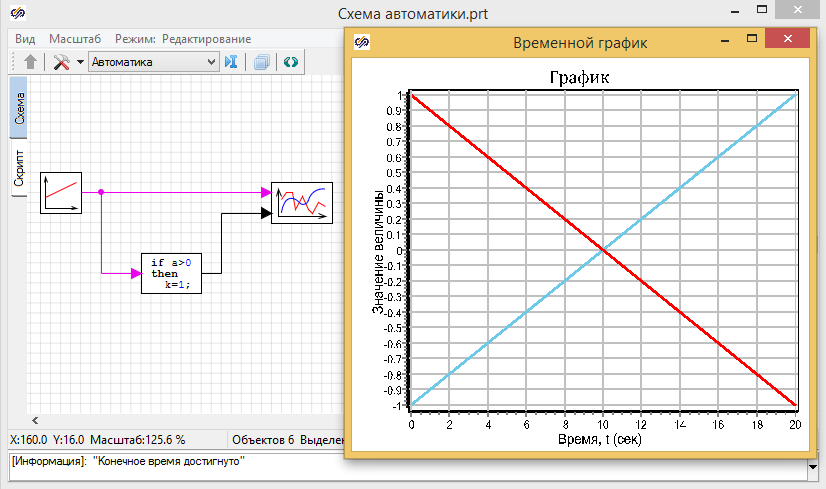
.Рис. 2.4. Окно SimInTech после расчета модели.
Ну вот в принципе вы и слепили свой первый блок-программу. Правда, крест этот на
хрен никому не нужен, поэтому сделаем полезную вещь, которую можно юзать, а
именно, расчет функции принадлежности µ(x) типа кривой Гаусса. Формула для расчета известна:
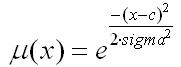
Чтобы забацать эту формулу, необходимо
ввести в программу две переменные с и sigma, и
записать код для расчета кривой.
Измените текст в блоке язык программирования на следующий:

Для увеличения наглядности используйте блок фазовый портрет из
закладки Данные. К верхнему входу фазового портрета подключите
выход линейного блока, а к нижнему выходу языка программирования. Смотри рисунок:
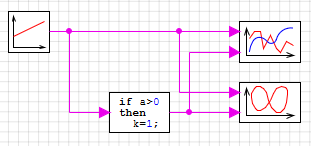
рис. 2.5.Схема для расчета функции принадлежности.
Запустите расчет, на графиках появилась шишка смотри рис. 2.6.
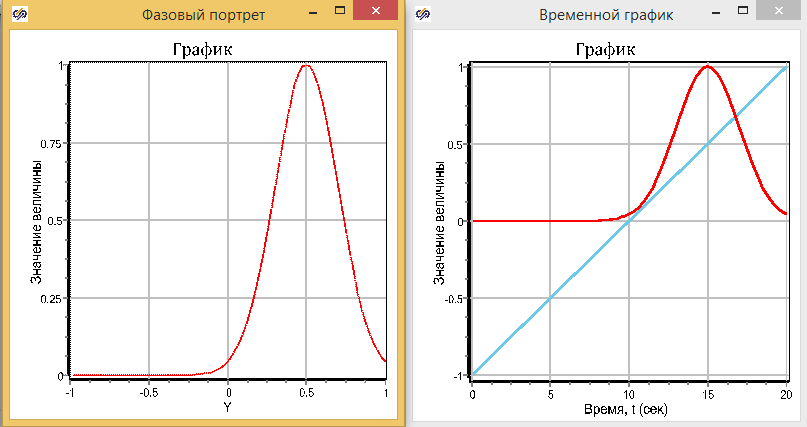
рис. 2.6.Графики расчета функции принадлежности.
Две переменный с и sigma определяют вид кривой: с - это значение, при котором
функция принадлежности равна единице - верхушка шишки. Sigma – параметр ширины шишки.
Таким образом мы получили блок, который позволяет рассчитывает функцию
принадлежности для входной величины. Из графиков видно, что в момент времени,
когда входная переменная
х = 0.5 (наклонная кривая) функция принадлежности равна единице, и чем больше х
отличается от 0.5 тем меньше функция принадлежности. Имея такой блок уже сейчас
можно скопировать его на схеме получать разные функции принадлежности для разных
термов забивая разные значения с и sigma.
Но мы как Ленин пойдем другим путем, все храбрецы всегда идут в обход.
Мы не
будем засирать рабочие поле схемы хуевой тучей блоков, как это делается в
Simulinke.
Мы сделаем из одного сигнала три терма с тремя функциями принадлежности в одном
блоке.
Для этого запишем функцию принадлежности как функцию. Измените текст на
следующий:

Запустите на счет и убедитесь что ничего не изменилось. А теперь воспользуемся
тем счастливым обстоятельством что, в SimInTech почти все, что может быть векторезировано,
является вектором. Следовательно, и переменные могут быть векторами. Пусть, в
базе правил нечеткой логике используем три терма низкий нормальный и
высокий.
Соответственно вместо одного значения на выходе нужно три, каждый из которых
показывает насколько величина является, низкой нормальной или высокой. Делается
это легко и не принужденно.
Переколбасим переменные с, sigma и выход
у в массивы из трех элементов соответственно c[3], sigma[3], у[3]. Запишем для каждого трема свои
параметры функции принадлежности. И чтобы уже совсем чувствовать себя сухо и комфортно
сделаем присвоение значений переменным в блоке инициализации (между слов
initialization и end). Это блок выполняется только одни раз при запуске расчета,
незачем повторять присвоение на каждом шаге интегрирования. А теперь в цикле ровно три
раза, как не давала зараза в одной тупой песне, вызовем функцию принадлежности. Текст
всего этого приведен ниже:

Если сейчас нажать на кнопку старт, то SimInTech покажет вам большую дулю
и сообщит что не может привести в соответствие какие-то размерности. Не
пугайтесь с вами добрый доктор проктолог, дело в том, что фазовый портрет должен иметь
на обоих портах одинаковую размерность, а у нас переменная, попавшая в язык
программирования расплодилась. Необходимо, размножить переменную подаваемую
на верхний вход фазового портрета. Возьмите в закладке Векторные
блок размножитель, и воткните его на схему, как показано на рисунке, а в качестве параметров запишите 3#1.
Теперь переменная преобразуется в
вектор из трех одинаковых значений и фазовый
портрет престанет глючить:
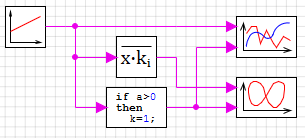
Рис. 2.7. Схема демонстрации фазификации.
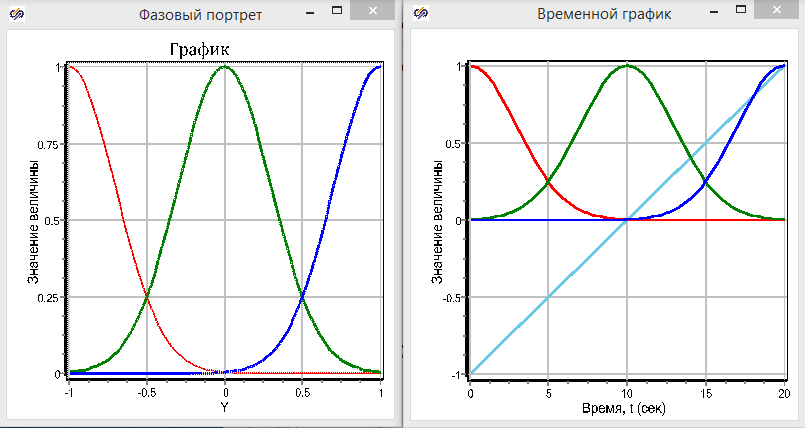
Рис. 2.8. Результаты работы блока фазификации
Посмотри еще раз на дело рук своих. Мы создали блок который обеспечивает анализ входной переменной и ее разложение на 3 терма (низкий, нормальны, высокий) (фазификацию). Мы посмотрев в потолок решили, что -1 это нихрена (low), 0, это ничего (normal), 1 это дохера (high). В нашей тестовой схеме переменная меняется от - 1 до 1. Запустив расчет мы наглядно видим как изменения линейные изменения одной переменной от - 1 до 1 приводят к изменению значений трех термов, в диапазоне от 0, до 1. В начале когда входная величина равна -1, терм нихрена имеет функцию принадлежности = 1, термы ничего и дохрена по нулям. по мере роста входной величины, значение терма нихрена уменьшается (величина еще низкая но уже не стопудово.), а значение терма ничего начинает расти, чем ближе к 0, тем ближе значение терма ничего к 1. Так на наших глаза простой рост входа от -1 до 1, не имеющий никакого смыла превратился в наглядный жизненный процесс перехода от нихера, через ничего к дохрена.
В это разделе мы рассмотрим покажем как из нихера сделать дохера c помощью SimInTech. Мы тут не изобретаем велосипед, а просто демонстрируем сеанс магии с разоблачением. Если вы захотите купить библиотеку нечеткой логики у MatchWork, то вам выкатят цену $7000, и будут заливать, какие продвинутые яцеголовые американские профессора делали эту библиотеку и какое это счастье всего за $7000 получить инновационный продукт передовой американской мысли. Дешевле только даром. На самом деле все эти библиотеки делают, китайцы и индусы будучи студентами университетов, а MatchWork просто рубит капусту с доверчивых лошар.
В среде SimInTech вы можете создавать свои библиотеки и даже продавать их. Покажем как это делается на примере библиотеки нечеткой логики. На предыдущем этапе мы создали блок который осуществляет фазификацию входной переменной на три терма, понятно что меняя константы в коде мы можем фазифицировать переменную на любое количество термов.Сейчас создадим блок, в котором пользователь будет задавать сколько нужно ему термов и какие значения им соответствуют. Что бы не кривыми ручками не поломать, то что уже работает, первым делом необходимо сменить название класса блока. Войдите в Свойства блока "язык программирования", который мы с вами сделали ранее, и замените тип элемента дав ему название "Фазификация Гаусса" (см. Рис. 2.9) Теперь при сохранении этого блока, мы не повредим существующий блок язык программирования, несмотря на любую рукожопость.
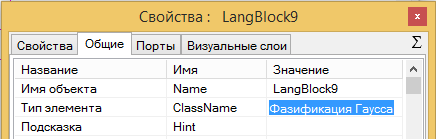
Рис. 2.9. Именуем новый блок
После того как тип элемента переименован, можно приступить его редактированию. Нужно убедится, что SimInTech знает, что перед ним находиться не лошара юзер, а крутой разработчик. Заходим в главное меню программы пункт "Файл" подпункт "Параметры" В появившемся окне нужно поставить галочку в опции "Режим разработчика" (Рис. 2.10)
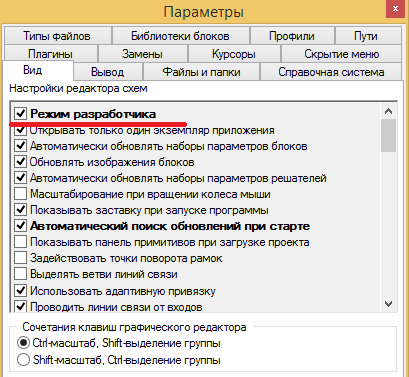
Рис. 2.10. Переводим систему в режим разработчика
В режиме разработчика выделяем блок "Язык программирования" на схеме и переходим к главному меню программы "Правка" в самом низу находится подпункт "Изменить блок", в диалоговом окне необходимо снести все свойства которые там могут быть (нам они уже не понадобятся) и добавить новые как показано на Рис. 2. 11. Для удаления и добавления используются кнопки внизу справа. В качестве свойств блока мы задаем Количество термов, Mассив значений с, и Массив значений sigma. Тут же мы даем значения по умолчанию (см. Рис. 2.11).
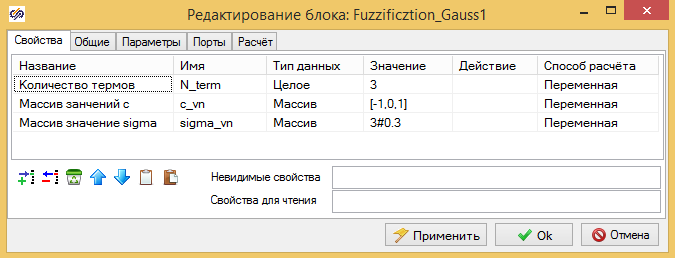
Рис 2.11. Параметры блока фазификация заданные разработчиком
Нажимаем кнопку окей. Если вы все сделали правильно, у нашего блока в свойствах появились ровно те же поля. Что посмотреть и поменять свойства выделите блок, правой кнопкой мыши вызовите всплывающее меню и выберите пункт "Свойства объекта" . В окне выберите закладку "Свойства" (см. Рис 2.12). И вот оно счастье, меняйте параметры и получайте разнообразные фазификации в любом количестве.
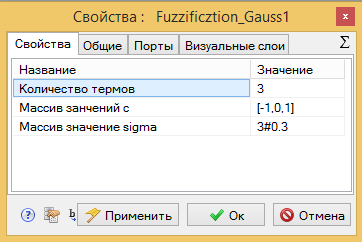
Рис 2.12. Параметры блока фазификация для пользователя
Перейдем в окно редактирования скрипта и изменим текст нашей программы с учетом, того что у нас появились новые переменные которые будут задавать счастливые пользователи нашего блока.
Вместо задания переменных в тексте программы сделаем присвоении их из переменных заданных пользователем. Добавляем защиту от отрицательного ввода кол-ва термов. Защита от дурака не когда не мешала, хотя нельзя предусмотреть изобретательность дурака. Сделаем еще одну защиту о выхода входной величины за границу диапазона. Поясню, если входная величина равна границе диапазона, то согласно алгоритму значения функции принадлежности для крайних термов равно единице. Однако, при выходе за границу диапазона значение функции принадлежности начнет уменьшатся, шишка Гаусса идет на убыль. Очень часто, это является ошибкой. Например, входная температура разбита на три терма: холодно +10 C, нормально +30 C, и горячо +55 C. Если температура 55 С это на 100% горячо (функция принадлежности = 1), и по правилам логики нужно максимально быстро крутить кран холодной воды, то при температуре 100 C, явно нужно делать тоже самое, хотя функция гаусса в этой точке может превратится в ноль. Чтобы этого не случилось введена проверка выхода значения входной величины за границу диапазона. Текст всего это лежит приведен ниже.

Теперь если сохранит это блок и запустить на расчет модель, графики должны быть точно такими как как на рис. 2.8. Если это так, то поздравлю вы только что разработали новый блок для SimInTech и сделали первый шаг к тому что бы стать миллионером. Что бы убедиться что это чудо произошло поменяйте свойства блока на другие и посмотрите какие графики у вас рисуются. Например, если для 5 термов, при параметрах заданных для блока, как на рисунке 2.13, у вас и графики похожи, то вы точно крутой разработчик, почти Цукамото или даже Мамдани!
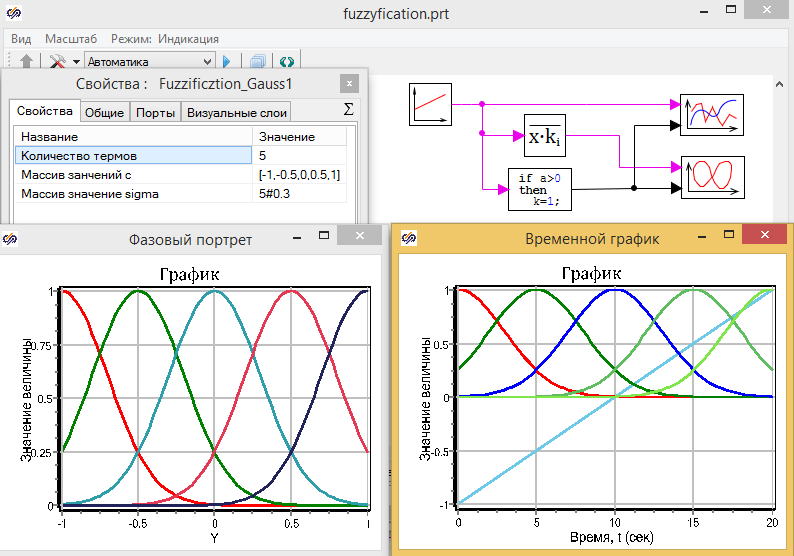
Рис. 2.13. Фазификация на 5 тремов функция гаусса
Теперь можно заносить этот блок в библиотеку, но перед этим изменим его свойства, что бы он был более похож на стандартные блоки SimInTech. Выделите блок на схеме, правой кнопкой мыши вызовите всплывающее меню и выберите пункт "Свойства объекта" . В окне выберите закладку "Общие" В нижней части списка можно можно изменить "Графическое изображение" и установить Да для параметра "Блокировка доступа". В этом случае при двойном клике на схеме по блоку будет вызываться окно с параметрами, а не текст программы (см. Рис. 2.14).
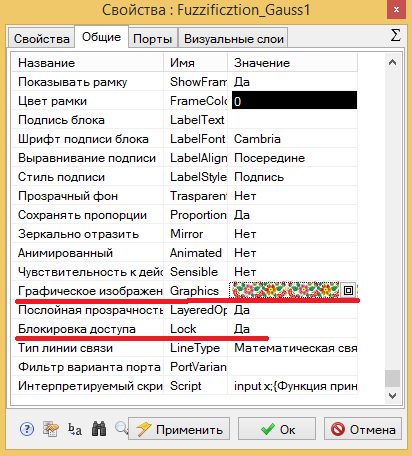
Рис. 2.14 Настройка блока фазификация перед добавлением в библиотеку.
Для занесения блока в библиотеку, выделяем его на схеме и в главном окне выбираем пункт меню "Файл" подпункт "Сохранить в библиотеку".
(Я бы еще рекомендовал "Сохранить в файл", что бы потом продавать это файл). Блок сохранился в библиотеку но мы пока его не видим в линейке. Еще раз меню "Файл", потом "Редактировать библиотеку". Пролистываем столбец "Все записи" и в самом низу находим наш блок "Фазификация Гаусса" (см. Рис. 2.15):
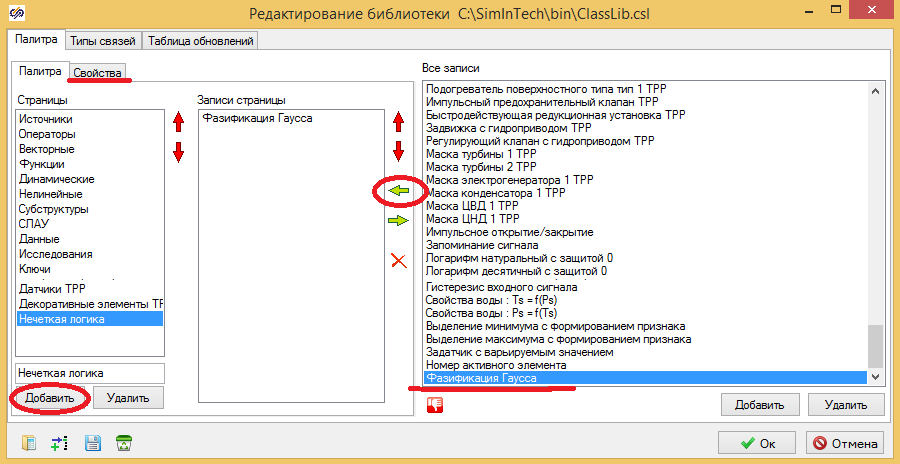
Рис. 2.15 Создание новой закладки "Нечетка Логика"
Ну вот последние клики мышкой и страницу "Нечеткая Логика" переносим в нее наш блок, на закладке "Свойства", задаем ему картинку и вуаля, у вас в палитре новая библиотека. (См. Рис. 2.16):

Рис. 2.16. Новая линейка блоков.
Прежде, чем перейти к овладению следующим этапам работы алгоритма
нечеткой логики, сделаем объект управления. Управлять будем дырявым баком, А Вы что хотели
ХУЯСом? Холодный Управляемый Ядерный Синтез (ХУЯС) мы рассмотри в следующий раз.
Управлять будем уровнем в дырявом баке. Задача проста как в школе про
бассейн,
в одну трубу вливается в другую выливается. Мы будем рулить расходом входа, а утечка
будет происходить самотеком
Параметры бака: высота - 2 м; Площадь сечения - 1 м; Диаметр выходного отверстия 0.05 м2.
Создайте новый проект, бросьте на схему Макроблок из закладки Субструктуры.
Войдите в блок и забейте в свойствах блока данные по баку:
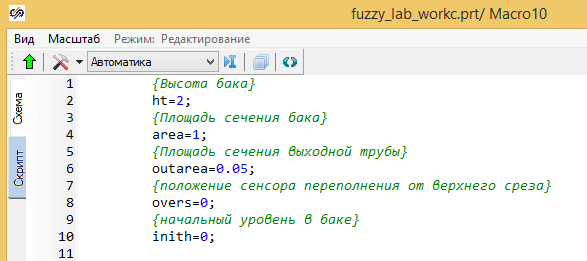
Динамику бака можно описать следующими уравнениями:
&
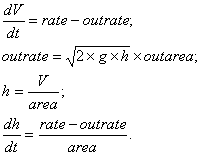
где: V - объем бака м3;
rate - расход поступающий в бак м3/с;
outrate - расход утечки м3/с;
h - уровень в баке м;
area - площадь сечения бака;
outarea - площадь выходного отверстия;
g = 9.8 - ускорение свободного падения.
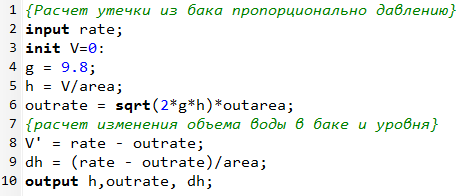

Рис. 2.17. Cхема суб-модели дырявого бака.
Разберемся теперь клапаном управляющим расходом. Основная идея такова. Задается номинальный расход 0.5 м3/с. Управляющие воздействие это скорость закрытия-открытия задвижки, интегрируя данную скорость мы получаем положение задвижки - число от 0 (задвижка закрыта - расход равен 0) до 1 расход равен номинальному. Зависимость расхода от положение задвижки линейная. Бросьте на основную схему новый Макроблок из закладки Субструктуры войдите в него и соберите схему как на рис. 2.18:

Рис. 2.18. Cхема суб-модели клапана.
Теперь модель объекта управления типа дырявый бак, готова к работе. Осталось положить на схему недостающие блоки, для задания уровня, отображения результатов. Конечная схема модели, вместе с регуляторному уровня на базе нечеткой логики будет выглядеть следующим как на рисунке 2.19:
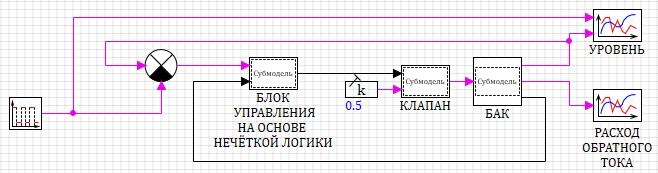
Рис. 2.19. Cхема суб-модели клапана.
Работа системы проста и незатейлива. Блок Меандр из закладки Источники задает изменение уровня с частотой 20 сек с 1.5 до 0.5, заданное значение сравнивается с реальным и разница подается на первый вход блока управления. На второй вход подается скорость изменения уровня в баке. На выходе мы получаем команду клапана который и управляет расходом в бак.
Получив модель дырявого бака, самое время перейти к рассмотрению базы правил нечеткой логики. Рассматривать будем сразу пока горячо. Для нашего бака правила блок управления на базе нечеткой логики имеет входные переменные уровень, и изменение уровня. Переменная уровень будет иметь следующие термы: 1 -высокий, 2 -нормальный, 3 -низкий. Переменная изменение уровня будет иметь такие термы: 1 - уменьшается, 2 -не изменяется, 3 -увеличивается. Блок управления клапаном будет выдавать переменную команда клапана, которая в свою очередь, будет иметь следующие термы: 1 -закрывать быстро, 2 -закрывать медленно, 3 -не менять, 4 -открывать медленно, 5 - открывать быстро. База правил для управления будет иметь следующий вид:
ЕСЛИ уровень = высокий TO команда клапана = закрывать быстро;
ЕСЛИ уровень = нормальный TO команда клапана = не изменять;
ЕСЛИ уровень = низкий ТО команда клапана = открывать быстро;
ЕСЛИ уровень = нормальный И изменение уровня = уменьшается ТО команда клапана = открывать медленно;
ЕСЛИ уровень = нормальный И изменение уровня = увеличивается ТО команда клапана = закрывать медленно;
Как видим на словах все абсолютно ясно и просто. Поскольку логика у
нас нечеткая, для каждого правила нужно, не просто получить
ответ да или нет, а рассчитать степь истинности. Для правил 1-3 степень истинности равна величание функции принадлежности
для соответствующего терма. Попросту, если уровень h высокий на 0.5
(µhigh(h) = 0.5) то и степень истинности равна 0.5. Функциональная схема макроблока реализующего данное правило:
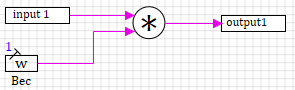
Константа
вес позволяет задать весовой коэффициент для правила в базе данных.
Создайте новый макроблок, свяжите эту схему и пометите его в архив схем с
многозначительным именем =>.
Степень истинности правил 4 и 5 зависит от двух входных переменных, соединенных
логическим И, если хотите понтануться, можете называть это логической
конъюнкцией. Для вычисления степени истинности существует несколько вариантов,
мы используем метод алгебраического произведения
смотри схему субмодели:
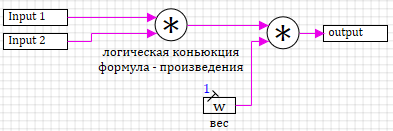
Эту субмодель тоже можно положить в библиотеку блоков на страницу нечеткая логика. Так вы постепенно приближаетесь к заветному богатству. Имея всего три блока можно уже начинать собирать систему управления на базе нечеткой логики. Возьмите блоки из нашей новой библиотеки и соберите схему как показано на рисунке 2.20.
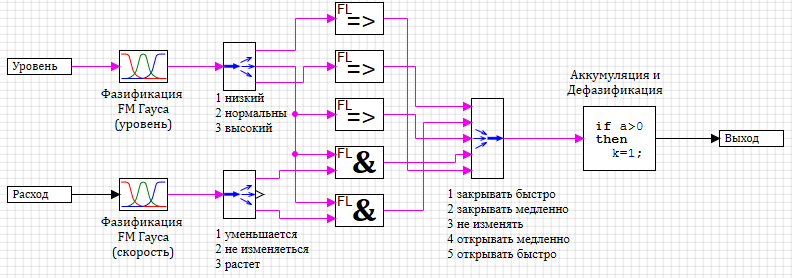
Рис. 2.20. Cхема регулятора на базе нечеткой логики.
На рисунке 2.10 картинки блоков для наглядности изменена, что совсем не влияет на функциональное наполнении блока. Возьмите блоки из архива схем и перетащите их на схему. Задайте параметры фазификации Гауса для переменной уровень: Количество термов = 3, Массив значений с = [-1,0,1], Массив значений sigma = 3#0.3 (три раза по 0.3); для переменной скорость изменения: Количество термов = 3, Массив значений с = [-0.1,0,0.1], Массив значений sigma = 3#0.03 (три раза по 0.03); Самая большая сложность на этом этапе, это соединение блоков фазификации и блоков правил в нужном порядке. Вот здесь и пригодится возможность подписывать блоки. Выход из блока фазификации для каждой переменной соедините с блоком Демультиплексор, для удобства дальнейшей работы с базой правил, подпишите под блоком соответствующие название термов в том порядке в котором они расположены в веторе. Ибо ORDNUNG, ORDNUNG UBER ALLES, как говорят немцы. Правда один мой знакомый немецкий фашист Патрик Вейс считает, что превыше всего penis enlargement, но я склоняюсь к мнению, что он слишком много смотрит качественной немецкой порнухи. Поместите на схему необходимое количество блоков правил. Выходная переменная имеет пять термов их мы будем предавать в виде вектора. Поместите на схему блок Мультиплексор и задайте 5 входных параметров. Подписи под блоком помогут правильно подключить результаты блоков правил. Помните ORDNUNG, ORDNUNG UBER ALLES! Соедините схему согласно записанных правил, как показано на рис. 2.20. И сохраните заготовку.
Получив вектор состоящий из пяти заключений из правил нечеткой логики, необходимо рассчитать
значение
выходной переменной. Для этого мы воспользуемся алгоритмом Мамдани.
Для начала осуществим фазификацию
выходной переменной на пять термов с помощью треугольных функций
принадлежности. Как Вы уже догадались мы снова будем
пользовать блок Язык программирования. Первая часть
текста программы приведена на рисунке 2.21

Рис. 2.21. Треугольная функция принадлежности для термов вывода
action[5] - это массив входных значений
(заключений из базы правил), который в процессе моделирования мы получим из
блока Демультиплексор;
TriangleFM - треугольная функция принадлежности.
var x=0; объявление переменной для тестирования функции, непосредственно в окне реадактора.
За что инженеры физики уважают MachCad? Не в последнюю очередь за то, он позволяет проверить ту галиматью, которую записывают в расчетах непосредственно в процессе записи. В любой момент можно построить графическую зависимость и посмотреть не припущеноли где возведение в степень, не стоил ли знак плюс вместо минуса или умножение вместо деления. А вот при программировании постоянно приходится вооружившись дебаггером шерстить код на предмет ошибок. Явно смущаясь программисты пользуются языком пиндосов называя это процесс поиском багов. Впрочем оставим поиск насекомых для обезьян и программистов и вернемся к SimInTech.
Чтобы убедится в отсутствии мондавошек в написанном куске кода, построим график функции. Для этого нажмите на кнопку ![]() построить графическую зависимость. При этом появится диалоговое окно построения зависимости как на рис. 2.22, Вообще то это окно предназначено для обработки векторных данных, но если поставить галочку в окошке Скалярная зависимость, то "легким движением руки шорты превращаются в ..." графопостроитель. В верхней строке задаете минимальное, максимальное значения по оси их X и количество точек графика. В нижнем записываете функцию которую только что запрограммировали. Нажимаете кнопку ОК и видите результат как на рис. 2.22:
построить графическую зависимость. При этом появится диалоговое окно построения зависимости как на рис. 2.22, Вообще то это окно предназначено для обработки векторных данных, но если поставить галочку в окошке Скалярная зависимость, то "легким движением руки шорты превращаются в ..." графопостроитель. В верхней строке задаете минимальное, максимальное значения по оси их X и количество точек графика. В нижнем записываете функцию которую только что запрограммировали. Нажимаете кнопку ОК и видите результат как на рис. 2.22:
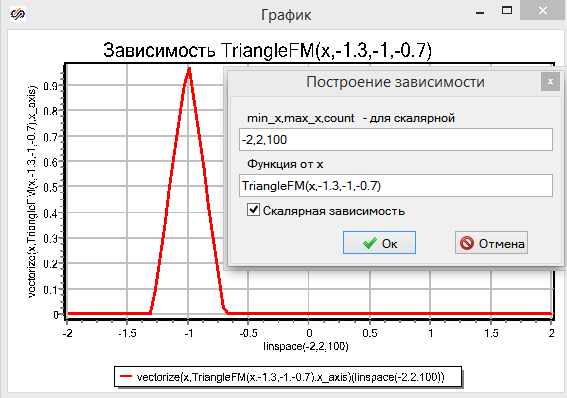
Рис. 2.22. Проверка работы функции графопостроителем.
Теперь меняя значения параметров функции (a,b,c) и нажимая кнопку ОК можно получать графики функции при различных параметрах. Следующая часть листинга приведена на рисунке 2.23. Здесь описываются параметры необходимые для нечеткого вывода:

Рис.2.23. Задание параметров для нечеткого вывода
Параметры a[i], b[i], c[i], задаются с учетом расположения заключений правил в входном векторе смотри рис 2.10. В примере принято расположение термов по возрастанию. В принципе, расположение может быть любое. Главное соблюдать соответствие между индексом терма в векторе входа, и индексом параметров функции принадлежности терма. Соответствие термов и параметров их функций принадлежности приведены в таблице:
| Index | Терм | Параметры функции принадлежности |
| 1 | закрывать быстро | (-1, -0.9, -0.8) |
| 2 | закрывать медленно | (-0.6, -0.5, -0.4) |
| 3 | не изменять | (-0.1, 0, 0.1) |
| 4 | открывать медленно | (0.3, 0.4, 0.5) |
| 5 | открывать быстро | (0.8, 0.9, 1) |

Если сейчас запустить построитель зависимостей и построить зависимость для AccProb, то мы получим график как на рис. 2.24. Функция объединила все треугольники теремов, при этом высота треугольников, стала зависеть от значения вектора action, значения которого мы присвоили в секции инициализации (см. рис. 2.23) во время моделлирования эти значения будут поступать из блоков расчета правил нечеткой логики, и в каждый момент времени моделирования высота треугольников будет соответствовать результатам логического агрегирования, соответствующих правил.
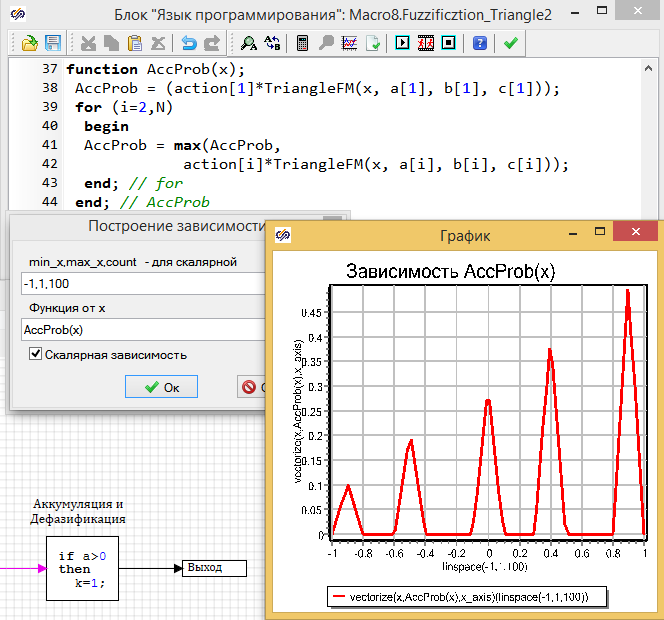
Рис.2.24. Расчет аккумулирующей функции
Таким образом, получив на вход 5 значений вычисления логических правил, и имея треугольные функции принадлежность мы создаем кривую из которой мы должны получит единственно значение выходной величины, для в алгоритме Мамдани, предлагается вычислить центр тяжесть полученной фигуры. Кривая у нас в виде функции AccProb(х) и мы находим центр масс полученной фигуры. Для этого нам и пригодится значение dX, рассчитанное в секции initialization блока см.рис. 2.23 Формулу расчета центра масс знает каждый октябренок:
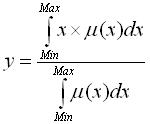
Ну, а численный алгоритм реализующий эту формулу методом треугольников представлен на рисунке 2.25

Рис.2.25. Дефазификация методом Мамдани.
Если вы правильно переписали листинги кода с рисунков выше по тексту, то при запуске расчета, на графике, подписанном нами как уровень, из основной схемы, (смотри рис. 2.19.) отразится изменения заданного уровня (синий график) и уровня обеспечиваемого регулятором нечеткой логики (красный график):
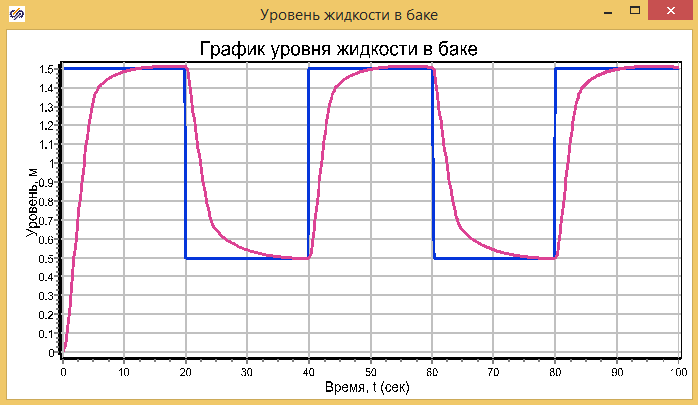
Рис. 2.26 Работа регулятора на базе нечеткой логике для регулирования уровня в дырявом баке.
Вот что мне не хватает в этом волшебном блоке, созданным за пару часов? А не хватает наглядности. Например если я ошибся в цифрах, запятую не там поставил. Есть конечно задроты программисты, как в матрице, которые глядя в цифры видят там голую женщину сиськи, жопы. И это хорошо, но для решения задачи желательно видеть не жопу, а форму кривой которую мы задаем в виде цифр, и желательно до моделирования и SimInTech это обеспечивает. Сейчас покажу как.
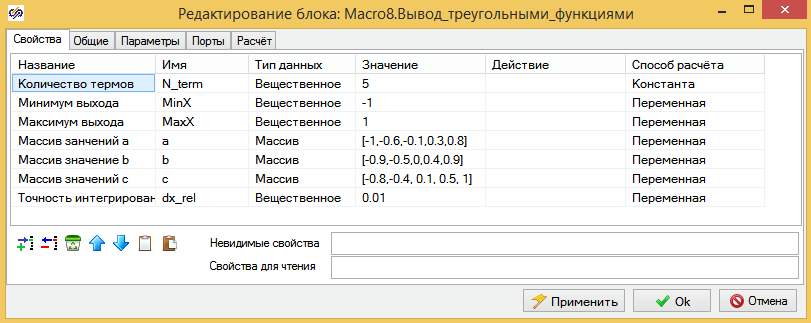
Рис.3.1Свойства блока нечеткого вывода треугольными функциями.
В п. 2.3 данной лабы описано, как создавать новый блок. Из нашего чудесного блока мы создаем новый задав ему имя "Вывод треугольными функциями". Что бы он стал универсальным, вы выносим параметры треугольных функция из текста программы в свойства блока, туда же отправляем в качестве параметров, количество термов, максимальное и минимальное значение выходной величины. Как это сделать см. п.2.3. В итоге свойства блока должны выглядеть так как на рис. 3.1 Значения по умолчанию берем из значений заданных в секции инициализации, в этом случае работа регулятора не должна измениться ни разу.

Рис.3.1Свойства блока нечеткого вывода треугольными функциями.
Как только вы задали эти свойства для блока, становиться абсолютно не нужным объявление этих переменных в тексте программы и можно смело их удалять. Секция инициализации программы сократиться до трех строчек кода:
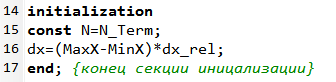
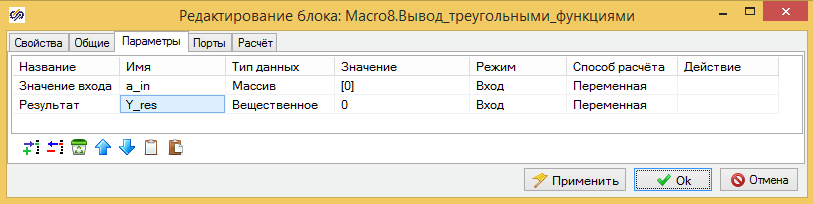
Рис. 3.2 Параметры блока нечеткого вывода треугольными функциями.
В тексте программы блока добавляем присвоение этим переменным:

Таки образом мы подготовили все для начала работы с анимационной системой SimInTech.
В принципе, все что мы будем делать дальше не будет относится к расчету и блок можно закрыть для доступа. Для этого в свойствах блока мы устанавливаем поле ""Блокировка доступа" - Да. После этого двойной клик по блоку будет вызывать окно свойств блока, а не текст скрипта. Потом всегда можно снять блокировку и поправить там, если что то пойдет не так.
Для того что бы оживить наш блок устанавливаем свойство ""Анимированный" - Да. В этом случае во время расчета будет вызваться и исполняться скритп на встроенном языке программирования, обеспечивающий анимацию изображения блока.
Установив эти поля, переходим в режим редактирования графического изображения блока, для этого в поле ""Графическое изображение" кликаем по кнопке вызова редактора. (см. рис 3.3)
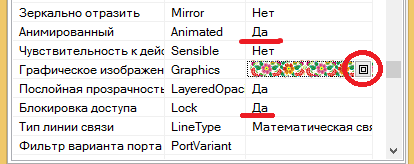
Рис. 3.3.Настройки блока нечеткого вывода
Внешний вид редактора изображен на рис. 3.4. Кроме этого на рисунке присутствует ""Панель примитивов" из которых можно собрать любое изображение (даже голую бабу), если есть художественный вкус. Тут же на рисунке есть окно редактирования объекта ""Свойства", в котором можно задать свойства этих примитивов. (см. рис 3.4)
Для вызова панели примитивов используется пункт меню ""Вид" подпункт ""Панель примитивов", редактор ""Свойства" вызывается нажатием правой кнопки мыши, при любом выделенном объекте в ""Графическом редакторе". На рис. 3.4 нарисована объект-прмимитив линия и показаны ее свойства.
Для успешного рисования нужно понимать, что окно редактирования содержит в себе, все то пространство, которое будет помещено в рамки блока на схеме. Все что ваше больное воображение нарисует в этом окне, будет нарисовано и на блоке в соответствующем масштабе. Вы можете настроить размер этого окна и масштаб отображения в нем любым способом как вам удобно.
Открыв это окно сотрите все, что там есть нафиг, на это не пригодится, настройте размеры как вам удобно рисовать и проведите линию по диагонали. Нахрена? Все просто, в свойствах это линии, можно прочитать размеры окна в условных единицах измерения. В моем случае свойства линии ""Координаты точек" показывают что высота данного прямоугольника по оси Y - 32 (от 16 до -16), а ширина по оси Х - 48 (от -24, 24). Таким образом можно догадаться что, центр координат находится в центре, а самое главное я теперь знаю, что для того чтобы мое изображение влезло в прямоугольник блока на схеме, оно должно быть иметь размер не больше (32 Х 48). После этого линию можно удалить.
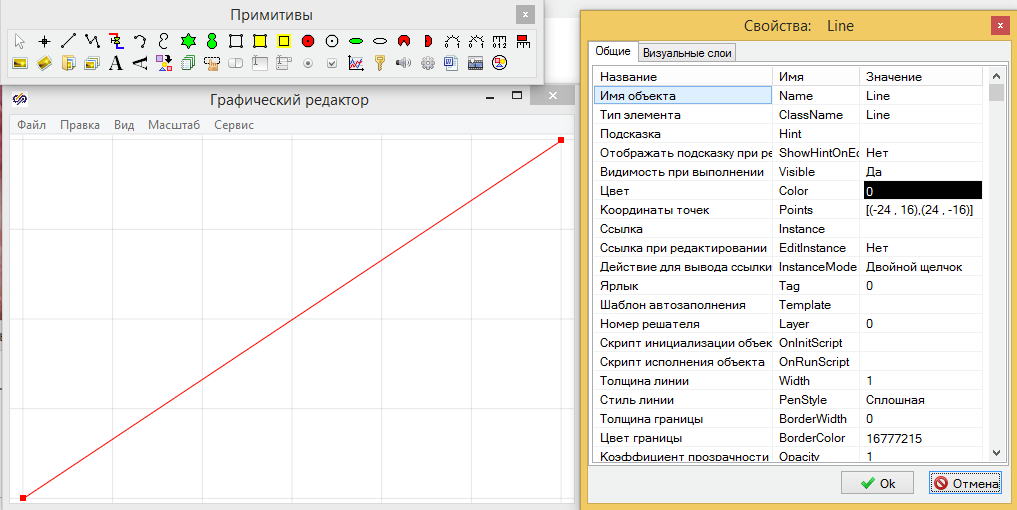
Рис.3.4. Проверка размеров изображения блока.
Для того, что бы наш блок мог отобразить функции принадлежности, нам необходимо передать в скрипт все параметры, по которым они рассчитываются. Делается это просто. В ""Графическом редакторе" выберем пункт меню ""Сервис" далее подпункт ""Cигналы", в появившемся диалоговом окне мы можем задать сигналы, которые будут использованы скриптом для рисования. Имена сигналов могут быть произвольными, но если задать имена сигналов совпадающих с свойствами блока, то автоматически их значения, во время расчёта будут забираться из свойств блока, что нам и требуется, поэтому просто повторяем, то что у нас есть в свойствах и не забываем параметры, который мы специально сделали и присвоили в скрипте блока для этой цели a_in и Y_res. (см. рис. 3.5)
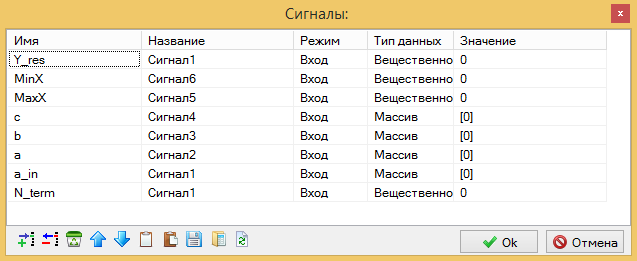
Рис.3.5.Сигналы передаваемые в скрипт для построения изображения.

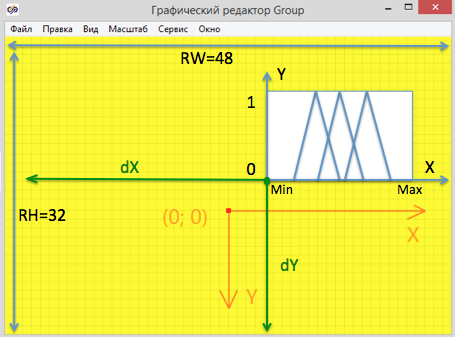
Рис. 3.6 Координатная сетка графического окна блока.
Для того что бы пересчитать величины расчетные в масштаб блока посмотрим на рисунок 3.6. Точка 0,0 находится в центре прямоугольника, направление координат показано красными стрелками (см. Рис. 3.6).Проще всего с координатой Y, поскольку функция принадлежности меняется от 0 до 1, то коэффициент масштабирования KY = - RH/1 (минус, потому что ось Y в графическом окне направлена вниз, см. Рис. 3.6), а для того что сдвинуть О к нижней границе блока DY = RH/2.
Для оси X коэффициент масштабирования KX = RW/(MaxX-MinX), а что бы сдвинуть MinX к левой границе блока нужно от текущего значения отнять DX = (MinX+(MaxX-MinX)/2)*KX (см. Рис. 3.6) Таким образом значение MinX окажется на левой границы изображения. Что бы не вычислять на каждом шаге коэффициенты мы это сделаем в секции инициализации. В итоге текст будет такой:

Ну и наконец, можно считать, что мы выполнив расчет коэффициентов съели овощи и теперь можно получить сладкое- начать рисовать треугольники. И рисовать мы будем не из примитивов и руками, а как настоящие программисты и скрипта и функциями. Задайте следующий текст в секции инициализации:

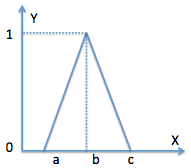
Что делают эти строчки, понятно из рисунка треугольной функции. Мы выбрали первую треугольную функцию i=1 и рассчитали координаты трех точек с помощью функций Хgrah и Ygraph, а потом создали примитив полигон использую стандартную функцию createprimitiv передав ему координаты точек в качестве параметров. Закройте окно нажав кнопку ""Применить", закройте ""Графический редактор", на вопрос ""Сохранит изображение?" отвечайте да, и будет вам чудо как на рис. 3.7 (Блок увеличен для наглядности). В поле блока вдруг откуда не возьмись появлялся треугольник построенный по точкам, заданным в параметрах блока и отмасштабированный в размер блока.
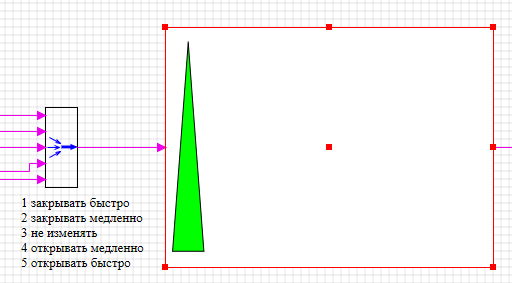
Рис. 3.7. Блок с треугольной функцией.
Если теперь менять значения a[1], b[1], с[1] в параметрах блока, то каждый раз будет рисоваться новый треугольник. Вернемся в графический редактор блока и удалим все что мы нарисовали.
И завершим создания анимации блока работы нечеткой логики.
И начнем мы в секции инициализации, и начнем с того что сотрем все что еще не нарисовали, поскольку каждый раз при инициализации и изменений параметров будут создаваться новые полигоны, нужно удалить старые что бы не засирать поле:

Данный кусок кода обратным счетом обходит все объекты и проверяет их имена, если имя содержит строку "Polygon_", то мы удаляем это объект на хрен. Так же в этом куске кода мы удаляем линию на всякий случай. Теперь наверняка все чисто и поле белое как снег и можно нарисовать столько термов, сколько задано в параметрах.
Создавая новые полигоны, мы присваиваем им имена начинающиеся на строку "Polygon_", это позволит нам в дальнейшем найти и удалить их на хрен при следуещей инициализации.
Поскольку мне не направиться зеленый цвет, я в коде меняю его на синий, и убираю линию границы полигона, мне она тоже не нравиться в итоге у меня получается следующий код:

Полигоны и треугольные функции это хорошо, но я хочу еще получить на схеме оценку выходной функции. Для этого я создаю линию, которая покажет где между максимум и минимум находиться результат нечеткого вывода:

На этом создание изображения блока закончено, закроем секцию инициализации словом end;
Если сейчас сохранить скрипт и закрыть окно подтвердив сохранения изображения, то изображение на схеме будет отображать наглядно параметры фазификации блока нечеткого вывода (см. Рис. 3.8).
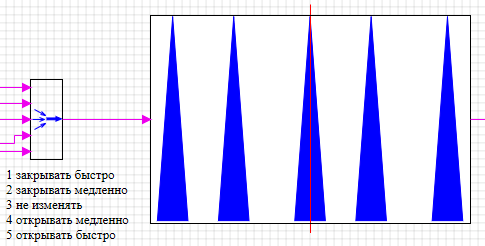
Рис. 3.8. Изображение блока фазификации
Ну и последний штрих оживление этих треугольников в процессе расчета. Текст ниже:

Все просто, если у нас проект находиться в состоянии расчёта, мы для каждого терма готовим массив точек треугольника, учитывая значения входных функций, тутто и пригодилась переменная a_in - она определяет высоту треугольника. По имени находим соответствующий полигон и устанавливаем ему новые точки.
С линией поступаем еще проще пересчитываем, координаты по результату вывода Xgraph(Y_res) и передвигаем ее в нужное положение. Если вы все сделали правильно, то ваш блок во время расчета отображает состояние нечеткого вывода. Что бы это увидеть установите синхронизацию в параметрах расчета с реальным времени (иначе расчет проскакивает так быстро что ничего не успеть увидеть)
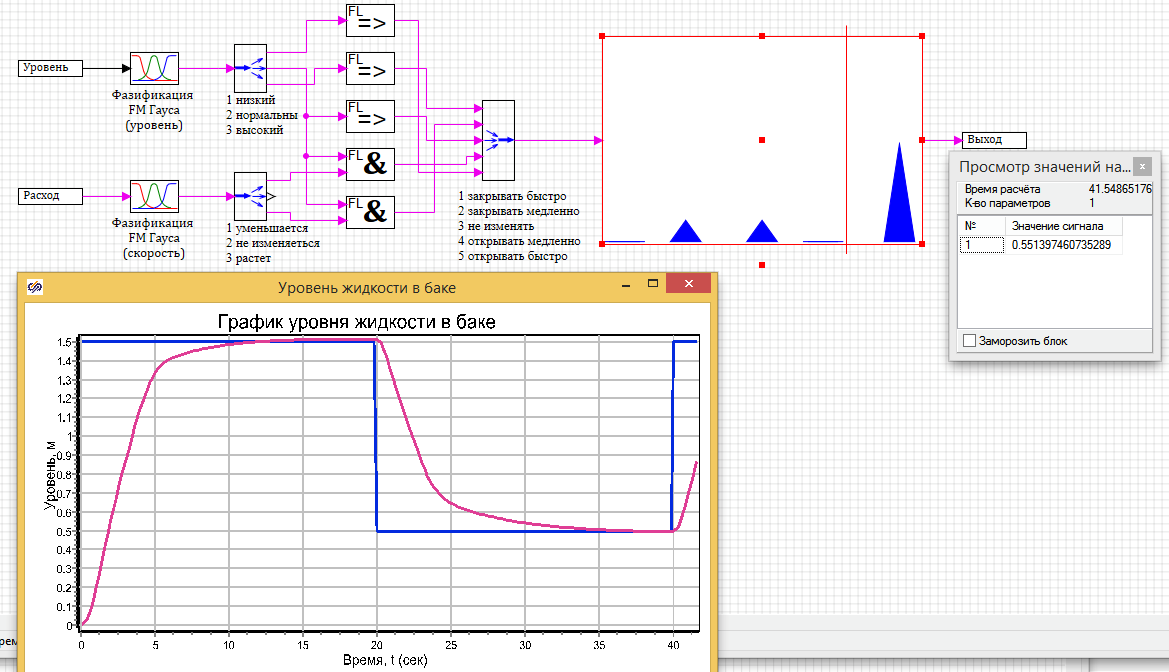
Поздравляю вы теперь не только создали блок нечеткого вывода но и создали наглядную анимацию работы этого блока непосредственно на схеме, в процессе расчета и подготовки данных.
Выполнив это лабораторную работу вы убедились, что нечетка логика это не просто, а очень проста.
Так же наглядно показано как создавать новые блоки в SimInTech.
1. Тимофеев К.А. "Описание языка
программирования SimInTech"
2. Козлов О.С. "Теория
автоматического управления. в примерах и среда моделирования ПК МВТУ".
3. Леоненков А.В. "Нечеткое моделирование
в среде MATLAB и fuzzyTECH"
1.Сайт SimInTech.
2. Последние версии SimInTech.
3. Архив с проектами на тему лабораторной работы.